Logic and
Categorical Claims
Standard Form Categorical Claims
Categorical Claims and Standard Form
(Format)
Categorical Claims and Quantity: Universal vs Particular
Categorical
Claims and Quality: Affirmative vs Negative
Categorical
Claims and Unit Classes
Categorical Claims and Venn Diagrams
Categorical Claims and the Square of Opposition
(Hypothetical View)
The Square of Opposition: Existential View
Categorical Claims and Distribution
Fallacious Reasoning Regarding Contraries and Contradictories
Formal Logic and
Categorical Claims
Let's
move on to the topic of Categorical claims.
I would like to read a quote:
"Like Moliere's M Jourdain who found that
he had long been speaking prose, I found that I had long been forming
propositions. `yes, I form propositions
when my tongue does more than wag. I
form them out of terms. I say something
about something. Therefore, I ought to
be able, in serious talk, to pinpoint those two parts of proposition. I ought to know exactly what I am talking
about, and exactly what I am saying about it.’[1]
A.
A. Luce
The
classical study of deduction is also called the Aristotelian study of
deduction. It was so names after the
Greek philosopher Aristotle (384-322 b.c.) Aristotle
and generations of logicians afterwards confined themselves primarily to the study
of certain kinds of statements, Categorical statements, the
relationships among these statements and arguments comprised entirely of these
kinds of statements. Aristotle and later
writers found that mentally moving from one group of statements to a certain
conclusion, when they are arranged in a particular way was good, correct,
logical. But certain mental movements
with different arrangements of statements were not good, not correct, illogical. They noticed patterns building up and the
relations between the patterns. This
they formalized into rules. These are
the rules of the categorical syllogisms that we will be studying.
Categorical
statements, claims, propositions, (I will be using these words interchangeably)
are claims about classes of things, that is, sets or categories. A class is a collection of objects that have
specified characteristic in common.
There are various ways in which one class may be related to another. If every member of one class is also a member
of a second, the first class is said to be included or contained in the
second. For instance, the class of blue
Toyotas is included in the class of cars.
However,
if only some members of the first class are included in the second, the first
is said to be partially contained in the second. For example, the class of blue Toyotas is
partially contained in the class of scratched cars. (That is, some blue Toyotas are scratched,
but not others.) There are some pairs of
sets that have no members in common.
These are disjoint sets, such as the set of all Toyotas and the set of
all melons. No Toyota is a melon and no melon is a Toyota.
Standard Form Categorical Claims
In
ordinary informal language, we can express categorical claims in all sort of different ways.
(E.g. All men are mortal. Every man is a mortal thing. If it’s a man then
it is mortal. Each man is mortal. Etc.)
But there
are just four standard forms of
categorical propositions. They exhaust the
possible logical relations that may occur between any two sets of things. They can be illustrated by the following
claims:
1. All A-s are B-s.
2. No A-s are B-s.
3. Some A-s are
B-s. (Where “some” has the technical meaning of “at least one.”)
4. Some A-s are not
B-s. (Again, meaning “at least one.”)
Note
that each of these categorical claims relate one category (in whole or part) as
indicated by the SUBJECT TERM (A-s) to
another category, indicated by the PREDICATE TERM (B-s) (either affirmatively or negatively).
Note
further that the verb in a standard form categorical, claim is always ”are” and
that both the subject and the predicate of a standard form categorical claim
must be plural nouns or noun-phrases.
Pop Quiz:
The claim “No cats are friendly.” Is NOT a standard form categorical
claim.
Why?
How could it be rewritten to express the same
content but be in standard form?
Categorical
Claims and Quantity: Universal vs Particular
If a categorical
claim makes a claim about the entire SUBJECT CLASS
it is called a UNIVERSAL CATEGORICAL Claim.
All Toys…
No
Fish…
All
Bugs…
No
people from Georgia…
If a
categorical claim makes a claim about one or more members of the SUBJECT CLASS,
but not every member of the subject class, it is called a PARTICULAR CATEGORICAL
claim
Some
Eggs…
Some
men…
Some
Lithuanians…
So all categorical claims are either: UNIVERSAL
or PARTICULAR
We
call this the QUANTITY of the proposition. And the words “All,” “No” and “Some” are the “quantifiers.”
Categorical
Claims and Quality: Affirmative vs Negative
When
a categorical claim asserts the existence of a relationship between the Subject
term and the Predicate term we say that the
proposition is AFFIRMATIVE.
When
a categorical claim denies the relationship between the Subject term and the Predicate
term we say that the proposition is NEGATIVE
All
categorical propositions are either: AFFIRMATIVE or NEGATIVE
We
call this the QUALITY of the proposition.
|
AFFIRMATIVE |
NEGATIVE |
|
|
UNIVERSAL |
(#1) ALL As are Bs |
(#2) NO As is Bs |
|
PARTICULAR |
(#3) SOME As are Bs |
(#4) SOME As are not Bs |
#1 is
a universal affirmative proposition. It
is about two classes. It claims that the
first class is included in the second.
#2 is
a universal negative proposition. It
denies that any A is a B.
Both
one and two are universal claims because they do claim something about each and every member of the subject class, or the “universe
class”.
Now
sometimes a person will define the universe they wish to talk about. He may only be talking about the universe of
married women, or of human car drivers or fish.
For clarity, we must determine specify the “universe of discourse” at
issue.
O.
K. We have gone over a universal
affirmative and a universal negative.
#3 is
an affirmative particular. It does NOT state something about each and every member of the subject class, but rather it affirms
something about some member of the subject class (and maybe only one member at
that).
#4 is
a negative particular.
It does NOT state something about each and every
member of the subject class, but rather it denies something about some member
of the subject class (and maybe only one member at that).
The
four standard forms may be written schematically as follows where S is the
subject class and P is the predicate class.
1.
All S are P
2. No
S are P
3.
Some S are P
4.
Some S are not P
If
you are asked to translate an English sentence into a standard from categorical
claim, It MUST conform to one of the four possible forms:
1.
All ___ are ___.
2. No
___ are ___.
3.
Some ___ are ___.
4.
Some ___ are not ___.
And remember
that only plural nouns (e.g. cats) or noun phrases
(things that are friendly) go into the blanks.
Categorical
Claims and Unit Classes
Sometimes
the class of things being discusses is a unit class (only one member). For instance, the sentence “Today is Monday.”
In NOT a standard form categorical claim, but it can be rendered
as a categorical claim. How? Well, I can convey the same information by
saying “All things identical to today are things that are
identical to Monday.” Thus, I
rendered the unit class claim as an universal, in this
case affirmative. Likewise, I can say
“Socrates is not a banana.” or express the same information as a standard from categorical
claim: “No things identical to Socrates
are things identical with bananas.” Since
“Socrates” names a unit class, we can treat this too as an
universal claim.
From
the time of its discoverer, Aristotle, until the nineteenth century,
categorical logic was the only
systematic logic. However, many refinements
were made to the basic theory during this period of over two thousand years.[2] We will next be covering the basics of this
system, but even the basics should prove helpful in our evaluation of arguments
and allow us to do a lot of logic.
Since
logic is a skill, like playing chess or poker, I recommend that you practice
diagraming categorical claims and check your own comprehension of the
material. If you have problems with it you are welcome to ask me if course.
Now,
categorical logic is based on standard form categorical claims. A standard form categorical claim is what
results when you put the words or phrases that name the classes which you are
talking about into the following structures:
1.
All ___________ are ___________.
2.
No ___________ are
___________.
3.
Some __________ are ___________.
4.
Some __________ are not _______.
The
Affirmative Universal is referred to as an “A” claim.
The
Negative Universal is referred to as an “E” claim.
The
Affirmative Particular is referred to as an “I” claim.
The
Negative Particular is referred to as an “O” claim.
To be
sure, these are not the way you will find most categorical claims in everyday
life. But it is very helpful to
standardize normal claims, to translate, so to speak, ordinary language categorical
claims into standard form. This makes
them easier to deal with and make the logical relations between the claims more
pronounced.
Sometimes
the translation into standard form will be easy; other
times more difficult. But this is a regimentation that I want
everyone to adhere to. If I ask for
an example of a categorical claim or argument, I want it in standard form, and
I will deduct points on a tests or quiz if you don't present them in standard
form.
The
phrases that go in the blanks are called terms; the one that goes in the first
blank is called the subject term and the one that goes in the second is called
the predicate term. Shades of eighth
grade English class eh?
Categorical
Claims and Venn Diagrams
One
way to view the "logical geography" of the standard-form categorical
claims is to use diagrams invented by John Venn, a friend of Lewis
Carroll. Perhaps, you have been introduced
to diagrams used in set theory; the Venn Diagrams are somewhat different. Most descriptions of Venn Diagrams introduce
the three symbols and the symbols are used to answer
the question: “Anybody home?”[3] That is, is the region empty or
occupied? The area inside the circle is
used to provide information on the members of the class in question, if there
are any. The area outside the circle represents all other individuals (the
complementary class) if there are any.
Note that the label for the things names by the set is written outside
the circle, even though "things” themselves, if there are any, would be
inside the circle.

1. A circle is used
to represent a subject class or a predicate class and is generally so labeled
with an S (subject) or a P (predicate). Putting
the name of the actual subject or predicate class next to the circle is
preferred. If the circle is BLANK, then we DO NOT KNOW is anything is in there or
not (e.g. whether anyone is home.)

2. Shading (or sometimes
many parallel lines) is used to indicate areas which are known to be EMPTY.
I.e., there are no individuals existing in a shaded area (nobody home). Be careful here. Shading does NOT mean full. It means EMPTY.
E.g.,
the diagram below represents the class of "Yeti."

3. The third symbol
used is an "X" which represents "at least one" or
"some" individual exists in the area in which it is placed. The diagram below indicates there is at least one
member in this class, "some thing." There is at least one member of this
category.
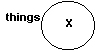
Again,
if the circle is blank, neither shaded nor containing an X then, for the purposes
of this course, we shall interpret that as meaning that WE DO NOT KNOW IF THE
SET HAS MEMBERSHIP OR NOT.[4]
Below
are four figures which represent each of the four categorical claims.
Figure
1# All Philosophers are Idlers.
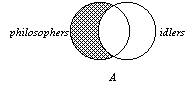
The region
to the left of center (region 1) is empty.
That is, the region which would contain “philosophers” who are NOT
idlers is empty. Why is that? Because the claim is that all philosophers
(if there are any) are idlers (within the Idlers’ circle).
Figure
#2 No Philosophers are Idlers.
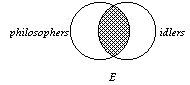
Here
the center region (region 2) is empty.
That is, the is region which would contain things that are BOTH
philosophers and idlers is empty. Why is
that? It is because the claim states at
there are no things that are BOTH philosophers AND idlers.
Figure
#3 Some Philosophers are Idlers.

Figure
#4 Some Philosophers are not Idlers.
Here
the center region (region 2) has at least one occupant.
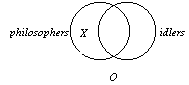
Here
the region to the left of center (region 1) has at least one occupant.
Figures
1 through 4 show the four standard form categorical claims represented by Venn
Diagrams, which are graphic illustrations of what the claims say. In the diagram the circles represent the
classes named by the terms, shaded areas represent areas that are empty, and
area containing x's represent a region which contains at least one member.
Notice
that he A-claim give us information about region 1 only, and no information about
region 2 or region 3.
An E
claim gives us information about region 2 but nothing about regions 1 or 3.
Likewise,
I claims only tell us about region 2 and O claims only
tell is about region 1.
For
the purposes of simplicity, logicians have adopted the custom of interpreting
the categorical word ‘some’ as meaning ‘at least one’. (and
so shall we.)
What
I would like to do now is take some examples of categorical claims and get some
practice in translating and diagraming them.
1. Only Athletes
are long distance runners.
2. Minors are
not eligible.
3. Every
salamander is a lizard.
4. Not every
lizard is a salamander
5. Not all
lizards are salamanders.
6. Only reptiles
can be lizards.
7. Frogs are the
only semiaquatic reptiles.
8. Frogs are not
the only semiaquatic reptiles.
9. Wherever there
are snakes there are frogs.
10. There are
frogs wherever there ore snakes.
11. The guy who
held up the bank is my next-door neighbor.
Categorical
Claims and the Square of Opposition (Hypothetical View)
Now
logicians love patterns. They also love
to classify. One of the ways they love
to set up the four categorical statement forms is in a square, and one of the classifications
they like to note about the categorical claims is whether or
not and which terms of the claim are distributed.
First,
let's set the categorical claims up in a square.
|
|
Affirmative |
|
Negative |
|
|
|
Square of Opposition |
|
|
Universal |
(A) All S are P |
|
(E) No S are P |
|
|
|
|
|
|
|
|
|
|
|
Particulars |
(I) Some S are P |
|
(O) Some S are not P |
|
|
|
|
|
The Square of
Opposition: Hypothetical View
This
is a nice lead in to our next topic, the Square of
Opposition.
The
square of opposition is concerned with the relation between the various
categorical claims. It is set up in the
way you see above. Now the relations between
the corresponding claims are dependent on the meanings of each of the
claims, and what implications can logically be drawn from them if they were
true. But when are they true? This is a very important question
and the answer is, to some extent, dependent on the view point you adopt when
you are evaluating the universal claims and what they mean.
Hypothetical View
and lack of Existential Import
Take
for example the claim, "All unicorns are horned creatures." First things first, what kind of categorical
statement is that? Well, clearly this is
an A claim. An
Universal Affirmative claim. Now is this
claim true or false? For the moment,
let's adopt the Hypothetical View of
interpretative Universal Affirmative claims.
On this interpretation we would read the sentence as follows:
For all things in the universe, if it
is a unicorn, then it is a horned creature.
This
is call the Hypothetical View point because you are NOT
claiming that there are in fact unicorns, but merely IF there are unicorns,
then they are horned creatures. This
statement can be true whether or not there are any
unicorns. And given what we mean by
unicorns, it in fact seems in fact to be true… under this Hypothetical View
interpretation.
A and I Claims.
Let's
assume that the statement is true. If it
is true that all unicorns are horned creatures (under this interpretation),
what can we know about the corresponding I claim: "Some unicorns are horned
creatures."?
Well, actually, nothing.
It is possible for A to be true while I is
false. Yes. This will happen in the case were there are no existing unicorns. Remember what the I-claim states. Since “some” means at least one existing thing,
the I claim is saying that at least one existing thing is a unicorn and is a
horned thing. But there are no unicorn.
(Sorry.) So then could A be true (If
there were unicorns they would all be horned things.) while
I is false? Yes.
And
can the A claim be true while the l claim is true? Yes. If
there were in fact unicorns (and all were horned creatures).
Thus the truth of the A claim tells us nothing
about corresponding the I claim. The
truth of A insures neither the truth not the falsity of I. Likewise, that the A claim is false tells us nothing
about whether the I claims is true or false. Further, knowing the truth value of the I claim,
tells us nothing about the truth value of A.
The
same lack of relations holds for E and O statements. On the hypothetical view, an E-claim is read,
“for all things in the universe, if it is an S then it is not a
P. For our example, when I claim "No unicorns are winged creatures." I should
be understood as meaning, "For all things, if it is a unicorn, then it is
not a winged creature.” The truth of the
E claim is compatible with the truth or the falsity of the corresponding O
claim. Likewise
the truth or the falsity of the O claim tell is nothing about the truth or the
falsity of the corresponding E claim.
Therefore, knowing the truth value of one, tells us nothing about the
truth value of the other.
A and E Claims
What
about the relationship of the A to the E on the hypothetical view? What are the truth conditions, that is what
does it take for the statement to be true?
For an A statement to be true means simply that if there are any
unicorns, they must have horns. They may
or may not exist, but if they do then they have horns. This
statement is only false if there ARE
unicorns, but they don't have horns.
That is the only time this
statement is false if you adopt the hypothetical viewpoint. So an A and E claims
could both be true as the same time? How?
They are both true if there were no unicorns.
Could
they both be false? Yes. How? If there ARE
unicorns and some of them have horns, but some of them do not. In that case, they are both false.
And of
course, if there are unicorns, one be true while the other is false.
So
again, knowing the truth value of one of the pair tells us nothing about the
truth value of the other. There is no
logical relation between them under the hypothetical view.
I and O Claims
What
about the relation between I and O claims on the hypothetical viewpoint. Could they
both be true at the same time? Yes. False? Yes. One true and the other false? Yes. So is there any relation going on here that allows us to
draw information of bout the truth value of one if we know the truth value of
the other? No.
A and O (and E
and I) Claims
Now
what set of statements have we not examined?
The relation between A claims and O claims and the relation between E claims
and I claims. Taking
the first pair first, if I know that that the A claim is true, then I know that
the O claim MUST be false. If I know
that, for all things in the universe, if it is a unicorn, then it is a horned
creature (The A claim on the hypothetical view), then I know that it CANNOT be
the case that at least one existing thing is a unicorn
and it is NOT a horned thing (the O claim on the hypothetical view).
Likewise,
if the O claim is true, then the A claim MUST be false. That is it cannot be
that all unicorns are horned creature AND that some unicorns are NOT horned creatures
at the same time. These claims cannot
both be true at the same time not can they both be false at the same time; they
MUST have opposite truth values. This is the logical relation of contradiction.
The
same relationship holds between E and I claims. They are saying exactly the opposite
tings. (Contradiction)
The
same logical relation of contradiction hold between E
and I claims.
|
|
Affirmative |
|
Negative |
|
|
|
Square of Opposition |
|
|
Universal |
(A) All S are P |
|
(E) No S are P |
|
|
|
|
|
|
|
|
Contradictions |
|
|
Particulars |
(I) Some S are P |
|
(O) Some S are not P |
|
|
|
|
|
The Square of
Opposition: Existential View
Now
suppose we change out interpretation from the modern, or Hypothetical View, to
the Existential View. This was the
interpretation favored by Aristotle and his ancient and medieval logician
followers, since they did not think it made a lot of sense to talk about the
relations of one empty set (non-existing things) to another. Truth conditions of the universal categorical
claims say that they are true only when each class has at least one member. This is called given universal categorical
claims “Existential Import.” Under this
interpretation, the categorical statements within the square are related in
numerous way.
All sorts of new logical relations pop up. Let's us consider the square with the
existential viewpoint. From this point
of view, this is how A and E claims should be diagrammed. Note, these diagrams indicate that the subject
class is not empty. As such, the A claim
implies the I claim and the E claim implies the O
claim. (See below.)

A and I Claims.
Let’s
first look at corresponding A and I claims. If it is the case that all unicorns are
horned creature AND there is at least one unicorn, then it MUST be the case
that some unicorns are horned animals.
Thus is the A claim is true, then the I claim
MUST be true. And note further that is
the I claim is false, then the A claim MUST be false. This is the logical relation of implication.
E and O Claims.
Let’s
next look at corresponding E and O claims.
If it is the case that No unicorns are horned creature AND there is at
least one unicorn, then it MUST be the case that some unicorns are NOT horned
animals. Thus is the E claim is true, then E claim MUST be true. And note further that is the O claim is
false, then the E claim MUST be false.
This is, again, the logical relation of implication.
A and E Claims
Now
let’s look at A & E claims. Could
they both be true at the same time? No. If there are unicorns and all of them are
horned creatures, then it cannot be the case that there are unicorns
and NONE are horned creature.
Could
they both be false at the same time? Yes. If there are unicorns, some of which are
horned creatures, others of which are not.
This is the logical relation of contrariety.
I and O Claims
How
about the relation between I and O statements?
Can the both be true? Yes.
See above. Can they both be
false? No. If there actually are
unicorns, then either at least one of them is a horned creature or it is not
(since we are assuming there has to be at least one.) This is the logical relation of sub-contrariety.
A and I and E and
O claims?
The
relationship of contradiction remains.
|
|
Affirmative |
|
Negative |
|
|
|
Square of Opposition |
|
|
Universal |
(A) All S are P |
<- Contraries -> |
(E) No S are P |
|
|
Implies
|
|
Implies
|
|
|
|
Contradictions |
|
|
|
|
|
|
|
Particulars |
(I) Some S are P |
<- Sub-contraries
-> |
(O) Some S are not P |
|
|
|
|
|
Now,
let me give you a set of definition:
Contradiction- a relation
between two statements which holds when both statements cannot be true at the
same time and cannot both be false at the same time.
Implies- One statement
is said to imply a second when the truth of the first is sufficient to insure the truth of the second and the falsity of the second
is sufficient to insure the falsity of the first.
Contrariety- a relation
between two statements which holds when both statements cannot be true at the
same time, though both may be false at the same time.
Sub-contrariety- a relation
between two statements which holds when both statements cannot be false at the
same time, though both may be true at the same time.
Seeing
the logical relation between the categorical statements will help us see what
movements are licensed as what are not.
But as you can see, it is important to determine under what truth
conditions an argument using categorical claims is being offered. Are the subject and predicate categories assumed
to be non-empty or not (Existential Import)?
This is important not only to determine the truth of the statements, but
also to determine what conclusions we may validly draw from those statements.
Moving Around the
Existential Square
If we
have the truth value of one of the four corresponding categorical claims, we
can always know the truth value of its contradictory. Many times we can
know the truth value of the other corresponding claims by using the Existential
Square of Opposition. For instance if we know that "All aluminum cans are
recyclable items." We immediately
know that its contradiction (O) is false.
We know that its contrary (E) is false and the contradiction of its
contrary (I) is true.
However,
on the Existential Square of Opposition we cannot always determine the truth
value of the other three remaining claims.
For example if we begin by knowing only that
the A-claim is false all we can infer is the truth value of the corresponding
O-claim. (T) Nothing follows about
either the E-claim or the I-claim. Since
the A-claim and the E-claim can both be false, knowing that the A-claim is
false does not tell us anything. Since
the I-claim and the O-claim can both be true, knowing the O is true does not
tell us anything about the I claim.
Some exercises:
Determine
as many truth values as you can using the Existential Square of Opposition.
1. Some mice are short tailed animals. (T)
2. No drugs are completely
harmless substances. (T)
3. Some evergreens are not
softwoods. (F)
4. All gardens are laborious
projects. (F)
5. No Muslims are Methodists.
(F)
Categorical
Claims and Distribution
Distribution
is best thought of as a function of telling the reader or listener something about
each member of entire class of things.
What classes? Well, the classes referenced
by the categorical claim (i.e. the subject class and/or
the predicate class). If something is
told about the each member of the subject class, we
say that the subject of the claim is “distributed.”
And
if something is told about each member of the entire predicate class, we say that
the predicate of the claim is “distributed.” Now if there is nothing being said about each
member of the class, then we say that the class/term is “undistributed.”
A Claims: All S are
P
What
does an A-claim tell us? It tells us
something about each and every S: that each is a
P. So S (the
subject) is distributed in an A claim.
But does the A claim tell us something about each and
every P? No. Thus the predicate
is said to be “undistributed” in an A claim.
E Claims: No S are P
What
does an E-claim tell us? Well, first, it
tells us something about each and every S: that each S
is NOT a P. So
S (the subject) is distributed in an E claim.
However, does the E claim tell us something about each
and every P? Yes. Each and very P is NOT an S. Thus, the predicate is also said
to be “distributed” in an E claim.
I Claims: Some S are P
What
does the I claim tell us? Does it tell
us something about each and every S? No.
Does it tell us something about each and every
P? No.
Thus NOTHING (neither the subject nor the predicate) is distributed in
an I claim.
O Claims: Some S are not P
So
far so good. This is all fairly straightforward.
A claim: subject
is distributed, predicate is not.
E claim: subject
is distributed AND predicate is distributed.
I claim: neither the subject nor the predicate is
distributed.
But we
run into some trouble with O-claims. It
is fairly easy to see why A-claims have distributed
subject terms. They clearly tell us
something about every member of the subject class. Since they do not tell us anything about the
entire predicate class, we say that they have an undistributed predicate
term.
E-claims
are relatively easy to understand as well.
They something about each and every member of
the subject class as well as something about each and every member of the predicate
class. In fact, if we were to Venn diagram
the reverse of the claim, "No apples are oranges." that is, if we
were to Venn diagram the claim, "No oranges are apples." we would end
up with pretty much the same diagram.
I-claims
do not give us much trouble either. It
doesn't take much time to realize that these statements tell us neither something
about the entire subject class nor something about the entire predicate
class. So then, neither the subject term
nor the predicate term is distributed in an I-claim.
O-claims
may give us some difficulty. I don't
know about you, I had a little difficulty getting clear
on this initially. What does an O-claim
state? Some S
are not P. Now, not surprisingly, the
subject term in an O claim is undistributed.
But, spoiler alert, the predicate terms of O claims is
said to be distributed. But why?
At
first it might be difficult to see what, if anything, the O claim has to say
about each and every member of the class of P. But consider this. If you knew that “Some saints were not men,” and
this was the only thing you knew, what is the one thing you could tell me about
each and every man?
There
is one thing you could tell me. Albeit, it is a minimal fact. The set of men is does not fully include the
set of all saints. That is, for each
member of the set, for each man, there is some saint to which that man is not
identical. But since this is something we can know about each and every man, the
predicate is distributed in the O claim.
Does
this mean that NO saints are men? Not
necessarily. If the O claim is true, the
E claim might be true, but it might be false as well. The I-claim might be true
or it might be false as well.
This
certainly does seem to correspond with our intuition about these claims. A universal claim says a lot. Hence the name. It only makes sense that when it is true,
many things should follow from it. So
too, a particular claim only intends to say something small, weak, negligible. When it is true it does just that, and few
things follow from it. But when it is
false, that is, when it doesn't even say the little it meant to, this, in a
negative sort of way, tell us something large.
But
to be clear, the predicate term in an O claim is said to be distributed.
Distribution
Chart
|
|
Subject
Distributed? |
Predicate
Distributed |
|
A
Claim |
Yes |
No |
|
E
Claim |
Yes |
Yes |
|
I
Claim |
No |
No |
|
O
Claim |
No |
Yes |
Implication,
Entailment, Contradiction, Contraries and Sub-contraries Chart:
|
Could
they both be true at the same time? |
Could
they both be false at the same time? |
|
|
No |
No |
Contradictions
|
|
No |
Yes |
Contraries |
|
Yes |
No |
Sub Contraries |
|
Yes |
Yes |
None of the
Above |
Implication Chart
|
If
the first one is true, could the second one be false? |
If
the second one is true, could the first one be false? |
|
|
No |
Yes |
The
first one implies the second one. |
|
Yes |
No |
The
second one implies the first one. |
|
Yes |
Yes |
No
Implication at all. |
|
No |
No |
Each
implies the other. They are
(logically) equivalent |
Four More Logical Relations: Transitivity, Symmetricity, Reflexivity
and Equivalence
Transitivity
A relation
R is transitive if
and only if (henceforth abbreviated “iff”), if x is
related by R to y, and y is related by R to z, then x
is related by R to z.
For
example, being taller than is
a transitive relation: if John is taller than Bill, and Bill is taller than
Fred, then it is a logical consequence of the fact that “taller than” is
transitive that John is taller than Fred.
A
relation R is intransitive iff, if x is related by R to y,
and y is related by R to z, then x is not related by R to z.
For
example, being next in
line to is an intransitive relation: if John is next in line to Bill, and Bill is
next in line to Fred, then it is a logical consequence of “being next in line”
is an intransitive relation, that John is not next in line to Fred.
A
relation R is non-transitive iff it is neither transitive nor intransitive.
For
example, likes is a non-transitive relation: if John likes Bill, and Bill
likes Fred, then, as a consequence of “likes” being non-transitive, there
is no logical consequence concerning John liking Fred.
Symmetricity
A
relation R is symmetric iff, if x is related by R to y,
then y is related by R to x.
For
example, being a cousin of is
a symmetric relation: if John is a cousin of Bill, then it is a logical
consequence of “being a cousin of” being a symmetric relation, that Bill is a
cousin of John.
A
relation R is asymmetric iff, if x is related by R to y,
then y is not related by R to x.
For
example, being the father
of is an asymmetric relation: if John is the father of Bill,
then it is a logical consequence of “being a the
father of” being an asymmetric relation, that Bill is not the father of John.
A
relation R is non-symmetric iff it is neither symmetric nor asymmetric.
For
example, loves is a non-symmetric relation: if John loves Mary, then, alas,
there is no logical consequence concerning Mary loving John.
Reflexivity
A
relation R is reflexive iff, everything bears R to
itself.
For
example, being the same
height as is a reflexive relation: everything is the same
height as itself.
A relation
R is irreflexive iff, nothing bears R to itself.
For
example, being taller than is
an irreflexive relation: nothing is taller than itself.
A
relation R is non-reflexive iff it is neither reflexive nor irreflexive.
For
example, loves is a non-reflexive relation: there is no logical reason to
infer that somebody loves herself or does not love herself.
Equivalence
A
relation R is an equivalence iff R is transitive, symmetric and reflexive.
For
example, identical is
an equivalence relation: if x is identical to y, and y is identical to z, then
x is identical to z; if x is identical to y then y is
identical to x; and x is identical to x.
Fallacious
Reasoning Regarding Contraries and Contradictories
No rocks are alive. Therefore, it follows that all rocks are
dead.
But this
does not follow. That is because “alive”
and “dead: are contraries, not contradictories. A failure to distinguish
between the two can lead to any number of logical errors in arguments.
If
two statements are contraries, then it is impossible for both of them to be
true,
but it is possible for both to be false. However, if two statements are
contradictories, however, it is impossible for them to both be true and
it impossible for them to both be false.
The
terms “alive” and “lifeless” are contradictories because everything either has
life (is alive) or lacks life (is lifeless), and thus nothing is both alive and
lifeless. The terms alive and dead are
contraries because nothing can be both alive and dead (cannot both be true of a
thing at the same time), but some things might be neither (can both be false of
thing at the same time). Dead implies
that it was once alive, but now it is not. Thus, the correct formulation of initial
statement would be:
No rocks are alive,
therefore all rocks are lifeless.
Because
of the technical and specialized nature of the fallacy, it is unlikely that you
will encounter it too often. If you do find this fallacy being used in a
real-world argument, please send it to me as an example.
