Section 4.1


Recall that if a line is rising left to right, it has a positive slope.
If a line is falling left to right, it has negative slope.

Horizontal lines have zero slope and vertical lines have no slope.

Also remember that the first derivative tells us the slope of the tangent line at a point.

If the graph of a function is rising from left to right, we say the function is increasing.
If you draw tangent lines at various points on the graph of an increasing function, all the lines will have positive slopes. This tells us that if a function is increasing, its first derivative will be positive.

If the graph of a function is falling from left to right, we say the function is decreasing. If you draw tangent lines at various points on the graph of a decreasing function, all the lines will have negative slopes. This tells us that if a function is decreasing, its first derivative will be negative.

A graph with curvature such as the one at right is called concave up. A concave up graph holds water. It is cup-shaped.
The spelling of cup should help you remember concave up.

A graph with curvature such as the one at right is called concave down. A concave down graph spills water. It is cap shaped.

Let’s see how we can use calculus to tell if a function is concave up. Look at the picture at right. Some of the tangent lines have positive slopes and some of the tangent lines have negative slopes. However, if we look from left to right, we see that the slopes start out negative, then get bigger and bigger, eventually becoming positive. Since the slopes of the tangent lines are increasing, that means the first derivative is increasing. 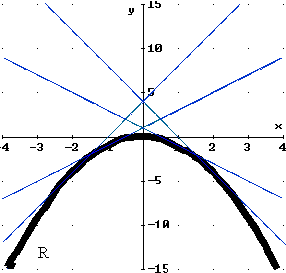If is increasing, then the derivative of is positive. But the derivative of is . Thus is positive when f is concave up.

Now we will see how to use calculus to tell if a function is concave down. Look at the picture at right. Some of the tangent lines have positive slopes and some of the tangent lines have negative slopes. However, if we look from left to right, we see that the slopes start out positive, then get smaller and smaller, eventually becoming negative. Since the slopes of the tangent lines are decreasing, that means the first derivative is decreasing. If is decreasing, then the derivative of is negative. But the derivative of is . Thus is negative when f is concave down.

An inflection point is a point where the graph changes concavity.
But just because a the second derivative changes sign does not necessarily mean you have an inflection point.
For example, the graph of the reciprocal function, y = 1/x, is concave down to the left of zero and concave up to the right of zero.
Yet zero is not an inflection point. It is an asymptote. To be an inflection point, an x-value must produce a corresponding y-value.
A graph can change concavity at an inflection point or a discontinuity.

If the graph of a function is rising from left to right, we say the function is increasing. If you draw tangent lines at various points on the graph of an increasing function, all the lines will have positive slopes. This tells us that if a function is increasing, its first derivative will be positive.
If the graph of a function is falling from left to right, we say the function is decreasing. If you draw tangent lines at various points on the graph of a decreasing function, all the lines will have negative slopes. This tells us that if a function is decreasing, its first derivative will be negative.

A graph with curvature such as the one at right is called concave up. A concave up graph holds water. It is cup-shaped. The spelling of cup should help you remember concave up.
A graph with curvature such as the one at right is called concave down. A concave down graph spills water. It is cap shaped.
Let’s see how we can use calculus to tell if a function is concave up. Look at the picture at right. Some of the tangent lines have positive slopes and some of the tangent lines have negative slopes. However, if we look from left to right, we see that the slopes start out negative, then get bigger and bigger, eventually becoming positive. Since the slopes of the tangent lines are increasing, that means the first derivative is increasing. If is increasing, then the derivative of is positive. But the derivative of is . Thus is positive when f is concave up.
Now we will see how to use calculus to tell if a function is concave down. Look at the picture at right. Some of the tangent lines have positive slopes and some of the tangent lines have negative slopes. However, if we look from left to right, we see that the slopes start out positive, then get smaller and smaller, eventually becoming negative. Since the slopes of the tangent lines are decreasing, that means the first derivative is decreasing. If is decreasing, then the derivative of is negative. But the derivative of is . Thus is negative when f is concave down.