Section 4.4

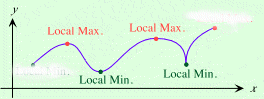
In section 4.2, we learned that a relative maximum was a y-coordinate greater than (or equal to) all the other y-coordinates “near” it.  Similarly, a relative minimum was a y-coordinate less than (or equal to) all the other y-coordinates near it.  Relative extrema are also called local extrema.

In this section, we learn that an absolute maximum is a y-coordinate that is larger (or equal to) all other y-coordinates in a given interval.  Similarly, an absolute minimum is a y-coordinate that is less than (or equal to) all other y-coordinates in an interval.

The absolute minimum in the picture above is also a relative minimum.  If we refer to a maximum or minimum without specifying whether it is local or absolute, we mean absolute.

The Extreme Value Theorem (Theorem 4.4.2 in your text) guarantees that every continuous function, when restricted to a closed interval, will have both an absolute maximum and an absolute minimum.  To find these extreme values, we use the 3-step procedure given in the blue box above example 1.

Example: Find the absolute maximum and minimum values of F on the given closed interval and state where they occur.

Solution:
Step 1:  By finding the derivative and setting it equal to zero, we see the critical points are 2 and –2.
Step 2:
F(-2) = -8 + 24 = 16
F(2) = 8 – 24 = -16
F(-3) = -27 + 36 = 9
F(5) = 125 – 60 = 65
Step 3: The maximum value is 65 at x = 5 and the minimum value is –16 at x = 2.

Example: Find the absolute maximum and minimum values of F on the given interval and state where they occur.

Solution: Here the interval is not closed so we cannot use the 3-step procedure given in the blue box in the text.   In fact, since the interval is not closed, the Extreme Value Theorem does not apply and we cannot even be sure if any extrema exist.  First we will try to rule out the existence of any extrema.

Since this tells us the graph shoots infinitely high, we know there is no absolute maximum.

This tells us that the graph is also shooting infinitely low, which means it doesn’t have an absolute minimum.  So F has no absolute extrema.