The Mean Value Theorem and Rolle's Theorem
Click here for an explanation of the two theorems in this section.
1) State the hypotheses of Rolle’s Theorem.
2) State the conclusion of Rolle’s Theorem.
3) State the hypotheses of the Mean Value Theorem.
4) State the conclusion of the Mean Value Theorem.
5) Consider the function f in the figure below.
a) Does f satisfy the hypotheses of the Mean Value Theorem on [5, 7]?
b) If the answer to (a) is no, state why. If the answer to (a) is yes, find
all values of c in [5, 7] that satisfy the conclusion of the Mean Value Theorem.
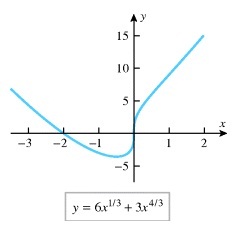
| 6) Consider the function f in the figure at right. a) Does f satisfy the hypotheses of the Mean Value Theorem on [-1, 1]? b) If the answer to (a) is no, state why. If the answer to (a) is yes, find all values of c in [-1, 1] that satisfy the conclusion of the Mean Value Theorem. c) Does f satisfy the hypotheses of the Mean Value Theorem on [0.5, 1.5]? |
 |
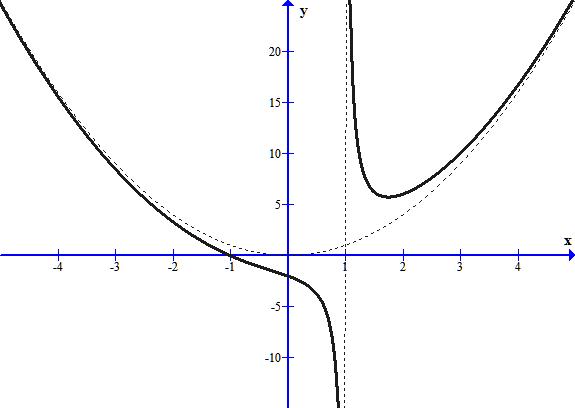
| 7) Consider the function f in the figure at right. a) Does f satisfy the hypotheses of the Mean Value Theorem on [0, 3]? b) If the answer to (a) is no, state why. If the answer to (a) is yes, find all values of c in [0, 3] that satisfy the conclusion of the Mean Value Theorem. |
 |
8) Give an example of a function that shows that the hypothesis f(a) = f(b)
= 0 is necessary for Rolle’s Theorem to be true.
9) Give an example of a function that shows that the hypothesis that f must
be continuous on [a, b] is necessary for Rolle’s Theorem to be true.
10) Give an example of a function that shows that the hypothesis that f must
be differentiable on (a, b) is necessary for Rolle’s Theorem to be true.
11) Give an example of a function that shows that the hypothesis that f must
be continuous on [a, b] is necessary for the Mean Value Theorem to be true.
12) Give an example of a function that shows that the hypothesis that f must
be differentiable on (a, b) is necessary for the Mean Value Theorem to be true.
13) True or False? Rolle’s Theorem is a special case of the Mean Value Theorem.
14) True or False? Rolle’s Theorem is a generalization of the Mean Value Theorem.
15) Is the following analogy true or false? Rolle’s Theorem is to the Mean Value
Theorem as the Pythagorean Theorem is to the Law of Cosines. (If you forgot
what the Law of Cosines says, read this.)
16) Let f satisfy the hypotheses of the Mean Value Theorem on [a, x]. Show
that
f (x) = f (a) + f ´(c) (x – a)
where c is some number that satisfies a < c < x.
17) Assume f satisfies the hypotheses of the Mean Value Theorem on [x1,
x2]. Show that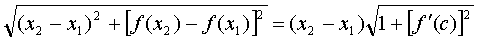
where c is in [x1, x2].
18) Suppose that f satisfies the hypotheses of the Mean Value Theorem and that
f '(c) is negative where a < c < b. Show that f (b) < f (a).
19) Let x0 < c1 < x1 < c2
< x2 < c3 < x3 and assume f satisfies
the hypotheses of the Mean Value Theorem for all x and that c1, c2,
and c3 all satisfy the conclusion of the Mean Value Theorem on the
corresponding intervals. Simplify:
f ´(c1) (x1 – x0) + f ´(c2) (x2
- x1) + f ´(c3) (x3 – x2)
Answers:
1) f is differentiable on (a, b), f is continuous on [a, b], f (a) = 0, and
f (b) = 0
2) There is at least one point c in (a, b) where f ´(c) = 0
3) f is differentiable on (a, b), f is continuous on [a, b]
4) There is at least one point c in (a, b) where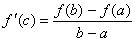 
5a) Yes 5b) c = 6
6a) No 6b) f is not differentiable at x = 0 6c) Yes
7a) No 7b) f is not continuous at x = 1 (or f is not differentiable at x =
1)
8) Answers vary. Any non-horizontal, non-vertical line on any interval will
work.
9) Answers vary. One possible answer is f (x) = tanx on [0, pi].
|
10) Answers vary. One possible answer is the function at right on the interval [-1, 1] |
 |
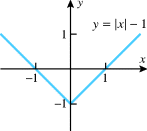11) Answers vary. One possible answer is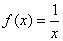 
on [-1, 1].
12) Answers vary. One possible answer is f (x) = |x| on [-1, 1]
13) True
14) False, the Mean Value Theorem is a generalization of Rolle’s Theorem.
15) True
16) 
f (x) – f (a) = f ´(c) (x – a)
f (x) = f (a) + f ´(c) (x – a)
17)
18)
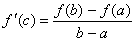
f (b)
– f (a) = f ´(c) (b – a)
f (b) – f (a) < 0
f (b) < f (a)
19)
f (x1) – f (x0) + f (x2) – f (x1)
+ f (x3) – f (x2) = f (x3) – f (x0)