The Definition of the Definite Integral
Let f be defined on [a, b].
Partition [a, b] into n not-necessarily equal subintervals by choosing n + 1 points a = x0 < x1 < x2 < ... < xn-1 < xn = b.
Let Δx1, Δx2, ..., Δxn denote the lengths of the resulting subintervals.
Let maxΔxk denote the norm of the partition.
Choose n arbitrary
points ![]() , one in each subinterval.
, one in each subinterval.
The
definite integral of f from a to b, denoted by ![]() , is defined to be
, is defined to be
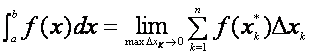
provided this limit exists.