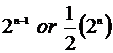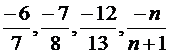Even Homework Answers

Even Homework Answers

Section 1.2

16a)

19, 22, 37, 3n + 1

16c)

32, 64, 2048,

16d)

18) 15 paths

22a) 19, 31, 50

22b) 6, 13, 33

22c) 8, 11, 30

26) 19 squares, 2n – 1

Section 2.2

16a)

Section 2.3

Section 3.1

4a) P = 33.05 in.
4b) 28.8 cm.
10a) d = 12 ft., r = 6 ft.
10b) d = 5.05 cm, r = 2.53 cm.
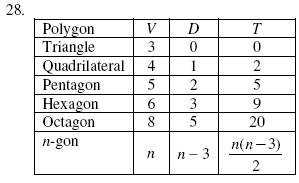
28) A = 20 sq. in. The area of the unshaded region is one-half the area of the total region.

Section 3.2

38) 1256 sq. ft.

Section 3.3

4a) 180m²

4b)

30) The sum of the areas of the 3 triangles equals the area of the trapezoid:

Multiplying both sides by 2 to get rid of the fractions:

ab + ab + c² = (a + b)(a + b)

2ab + c² = a² + 2ab + b²

Subtracting 2ab from both sides:

c² = a² + b²

Section 3.5

28a) volume of A = 125,000 cubic cm., volume of B = 125,000 cubic cm., volume of C = 125,000 cubic cm.

28b) surface area of A = 15,000 sq. cm., surface area of B = 17,500 sq. cm., surface area of C = 19,500 sq. cm.
28c) No
28d) Box A
52) 3.77 gallons

Section 4.1

18) True. The converse says: "If an angle is obtuse, then it measures 117 degrees. False.
26) False. The converse says: "If two angles are adjacent, then they share a common vertex." True.

Section 4.2

10) Not necessarily congruent (no AAA Congruence Postulate)
14) Not necessarily congruent (triangle HIL has SSA, not ASA)
22) D
24) CBA, ASA Congruence Postulate
26) C, CPCTC (Corresponding Parts of Congruent Triangles are Congruent)
35) Note that the segments in steps 2 and 3 should have segments signs over them.

Statements	Reasons
1. ABCD is a rhombus	1. Given
2. AB CD, ADCB	2. Definition of a rhombus
3. BDBD	3. Reflexive Property
4. ABDCDB	4. SSS Congruence Postulate

37) Note that the segments in steps 1and 2should have segments signs over them.

Statements	Reasons
1. Segments AC and BD divide each other in half	1. Given
2. AECE, BEDE	2. Definition of "divides each other in half"
3. angle BECangle DEA	3. Vertical angles are
4. BECDEA	4. SAS Congruence Postulate
5. angle DBCangle BDA	5. CPCTC

41) Note that the segments in steps 2 and 4 should have segments signs over them.

Statements	Reasons
1. ACF and AEB are right triangles	1. Given
2. ABAF, BCFE	2. Given
3. AB+BC = AF + FE	3. Adding = quantities to both sides of the equation
4. ACAE	4. Segment Addition
5. ACFAEB	5. HL Congruence Theorem
6. angle ACF angle AEB	6. CPCTC

46) The ropes are the same length so ADCD . The ropes are anchored the same distance from the base of the tree so ABCB .
Since DBDB , we know ABD CBD by SSS Congruence Postulate. Thus, angle ABD angle CBD by CPCTC. Since angle ABD and angle CBD are also adjacent and supplementary, they both measure 90°. Therefore, the tree will be perpendicular to the ground.

Section 4.3

9.Note that the segments in steps 2 and 5 should have segments signs over them.

Statements	Reasons
1. angle WVY angle WXYangle WYVangle XWY	1. Given
2. VWWY YX	2. If 2 angles of a triangle are , then the sides opposite those angles are .
3. angle VWYangle XYW	3. Each is 180 degrees minus 2 angles
4. WVY YWX	4. SAS Congruence Postulate
5. WXYV	5. CPCTC

11. Note that the segments in steps 1and 3 should have segments signs over them.

Statements	Reasons
1. PY & RX are altitudes PXRY	1. Given
2. PXR & RYP are right triangles	2. Definition of altitude
3. PRPR	3. Reflexive Property
4. PXR RYP	4. HL Congruence Theorem

13. Note that the segments in steps 1, 5, 7, 8 and 9 should have segments signs over them.

Statements	Reasons
1. BD is an altitude of ABC BD is the bisector of angle B	1. Given
2. angle BDA & angle BDC are right angles	2. Definition of altitude
3. angle BDA angle BDC	3. All right angles are
4. angle ABD angle CBD	4. Definition of bisector
5. BD BD	5. Reflexive property
6. ABD CBD	6. ASA Congruence Postulate
7. ADDC	7. CPCTC
8. BD is perpendicular to AC	8. Definition of altitude
9. BD is the perpendicular bisector of AC	9. Definition of perpendicular bisector

15. Note that the segments in steps 1, 2, 3, 7and 8 should have segments signs over them.

Given: ABC is isosceles with ABCB BD is a median Prove: BD is the perpendicular bisector of AC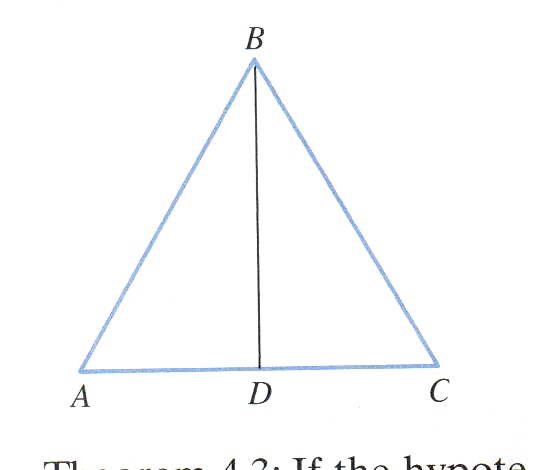
Statements	Reasons
1. ABCB BD is a median	1. Given
2. AD CD, BD bisects AC	2. Definition of median
3. BDBD	3. Reflexive property
4. ABD CBD	4. SSS Congruence Postulate
5. angle ADB angle CDB	5. CPCTC
6. angle ADB & angle CDB are right angles	6. Two angles that are supplementary are right angles.
7. BD is the perpendicular to AC	7. Definition of perpendicular
8. BD is the perpendicular bisector of AC	8. Definition of perpendicular bisector

22. The worker positioned board CD at the midpoint of board AB, so as long as the
distances AC and BC are equal, the boards are perpendicular by Theorem 4.10.

Section 5.1

2) angles 2 and 5, angles 9 and 12
4) angles 4 and 8, angles 6 and 14
12) angle 20
14) angle 4
32) angle 1 = 47°, angle 2 = 47°, angle 3 = 106°, angle 4 = 133°

Section 6.1

48) Width = 16.2 in., height = 21.6 in.

Section 6.2

26)