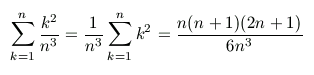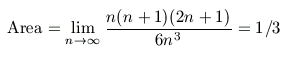Limits This animation [click 'refresh' or 'reload' to see it again] shows that after 7 steps the approximation is nearly exact. The right answer (1/3) should be the limit of our approx's. So far, we have three approx's to look at...1, 0.625 and 0.468 ... with no obvious pattern. In order to take a limit, we need to proceed more methodicly, we need a pattern, and we need some notation.

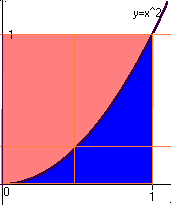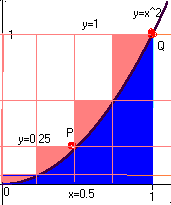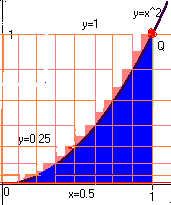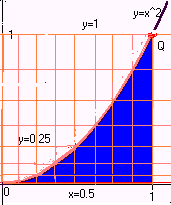
Let 'n' be the number of rectangles being used. Each rectangle has base = 1/n. The right endpoint of the base of the k-th rectangle is called x_k (so x_1 = 1/n, x_2 = 2/n, etc - see the picture below, where n=4). As before, we get the height of the rectangle by plugging x_k = k/n into y=x^2 [so, height = (k/n)^2]. So, its area is bh = k^2/(n^3). Now we use Sigma notation (and a theorem) to add all these areas up.

If you need some comic relief right now, let n=1 and see what you get. It should match the value of A we got using just one box (A=1). And n=2 should match the number under Picture 2 (previous page) which was 0.625. You don't really have to check this way, but it's nice to know we have found the right pattern.

Finally, we can get the exact area of the blue region by taking a limit as n (the number of rectangles) gets big.

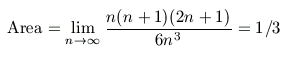
There is a bit more to say (and I did so in class!) but I'll just summarize it for now -

1. The sums we just used are called 'Riemann Sums'.

2. The limit we just took is (almost by definition) the integral of x^2 from 0 to 1.

3. We have some flexibility in how we choose the widths and heights of the rectangles. This requires more notation to explain (done in class), but it isn't even intended to help with calculations. It just makes the theory work (for example, the "abc thm").

4. Don't try this on a curve like sin(x). It would be too hard, and there IS a shortcut coming (the FTC).

5. Try to understand the C-A-L aspects of integration. You'll need that to know how to apply the method to other problems.

Back to Start

Back to Help Page