
INTEGRATION
INTEGRATION is a method of solving some fairly hard problems - about area, volume, length and work (etc). You always do 3 things - Chop, Add and take a Limit. This should be easy for any CALculus student to remember.
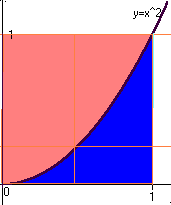
So how does it work? Teachers normally start by finding an area, since it is the easiest application. We wouldn't need integration to find a simple area, such as a rectangle [because then we know A=bh]. But any region with a curved perimeter is a lot harder. We'll use integration to find the area of the blue region shown below, which is under the graph of y=x^2, and above the interval [0,1]. You'll see that it's a pretty long problem. But eventually you'll learn shortcuts that can be written in a single line like this:

The symbol on the left is a definite integral. I'll try to explain what it means and why it equals the blue area. I won't try to explain the fast way to get the "1/3" yet. We will take a longer road that explains this chop - add - limit process called integration.
 |
 |
 |
 |
| A = 1 | A = .0125+.5 = .625 | A= [see below] = 0.46875 | A= [see below] |
First Approximations
1) The first step is to approximate the area (badly), by drawing a 1x1 box around it. This box has Area = 1, including the blue area we want, and the red area we don't want. See the first picture. Of course, A=1 is way too big. The good thing is that it was really easy.
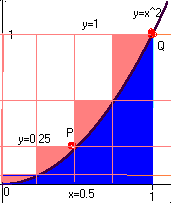
2) To improve our estimate, we'll Chop the box in two, along the vertical line x=0.5. On the left half, we'll use a rectangle of height 0.25, which is just tall enough to stay over the blue area. [How do I get 0.25? That's the height of the point P(x,y), where y = x^2 = (0.5)^2 = 0.25]. The area of this rect is bh = (0.5)(0.25)=0.125. For the right half of the box, we'll refer to Q instead of P, and use a height of 1^2=1, the same height as the original box. It's area is (0.5)(1)=0.5. We get the combined colored area in Picture 2 by Adding... 0.125+0.5=0.625. Since this still includes a lot of red area, it is still too big, but it is closer than 1.
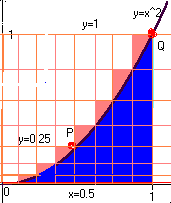
3) We Chop again at x = 0.25, and again at x = 0.75. We have 4 rect's now, and we choose the heights like we did before (see Picture 3). The widths are all 0.25. Adding (check me!), we get A = (0.25)(.0625+0.25+0.5625+1) = 0.46875.
4) Picture 4 shows the next step. Let's skip the numbers. We'd get something smaller than in step 3, but still bigger than the blue area. The next page has shows the first 7 steps in an animation.
written about 1/18/02, updated 1/23/02.