Tunisia


Mathematician Robert Osserman, 1926 - 2011, explores the Mathematics Behind the St. Louis Gateway Arch

In the beginning was the equation. It was born over three centuries ago, when mathematicians said that it described a beautiful curve: The surprising child of distinguished parents, the curve of exponential growth, and its companion curve of exponential decay, by taking equal parts of one and the other. Mathematicians called the curve described by their curve a catenary. Because - they said - it was the shape of a hanging chain, or a string of beads. Scientists said, if you take that catenary, and flip it over, it will make a perfect arch. Along came an architect who said, I have a vision of a magnificient arch that will be light and slender at the top, and will be strong and sturdy at its base, and will last as long as the arches built 2,000 years ago in Rome, and still standing today, and - may be - as long as the great pyramids, built 3,000 years before that. The engineer said, yes, we can do that. I will tweak your equation, and flatten your catenary, and I will tell you exactly how much to slim it down - from bottom to top. Then you will have a bright leaning arch that will reflect the white fluffy clouds and the blue sky. Planes will fly over it, birds will fly around it, and children will frolic. So, the architects, and the engineers, took the mathematicians' equations, and made drawings, and great columns of numbers, and took them to the steal-makers, and the construction crews. The dream became a reality: A thing of beauty, and a joy for at least a very very long time.



 

Problema Isoperimetricum
Problematum Ifoperimetricorum








Tanith stella, Alhambra, Espana

Selection of Key Full-Text Papers (Chronological)

History of Science Essays

Selection of Available Full-Text Books

Euler (1707-1783)

Jakob (also James or Jacques) Bernoulli (1654-1705)

Galileo Galilei (1564-1642)



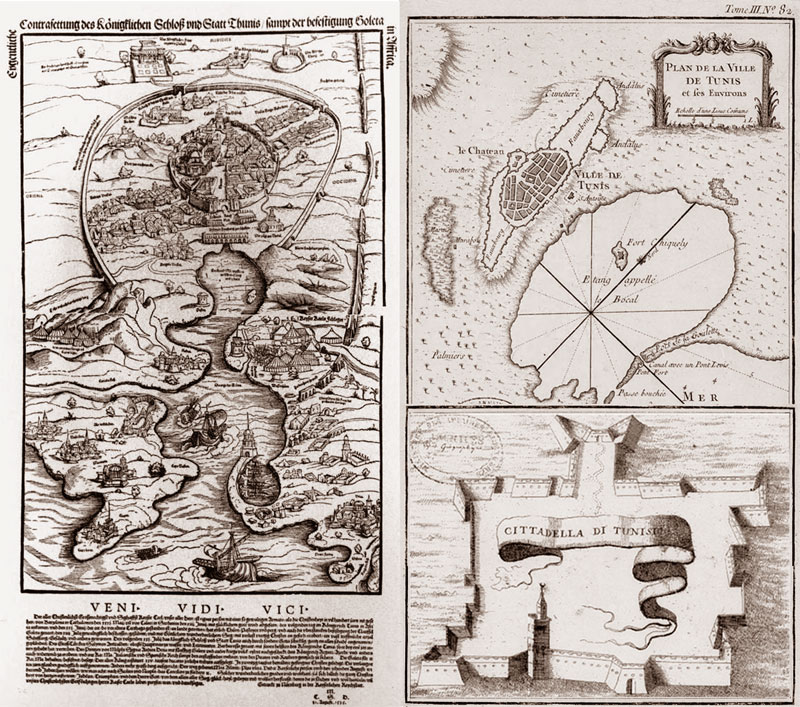
"Veni, Vidi, Vici" ("I came, I saw, I conquered"). Sketches of the double-walled city of Tunis and its surroundings from three different eras: Exactly on 31 August 1535, then from the mid-1600s and mid-1700s periods. The first is a commemorative woodcut carving by Erhard Schön (1491-1542) celebrating the conquest of Tunis by the Holy Roman King Charles Quint. The carving, in German, reads: "

Actual View of the Castle and the City of Tunis [Thunis], Including the Fortress Goleta, in Africa.
The text following Julius Caesar's triumphant invocation reads:

``The most Christian, most mighty, and victorious emperor Charles, the ruler of all of us, departed personally with an Armada, not seen in Christendom in many centuries, from Barcelona in Catalonia on May 31, and from Calari in Sardinia on 14 June. With favorable wind, he arrived in the kingdom of Tunis in Africa on the following day. On June 21 he stepped on land at the place known in antiquity as Carthage. He bombarded many gates, bastions, and hills, as well as attacked the overly strong fortification, known as Goleta, on July 14 gaining a divinely marvellous victory with the loss of only forty Christians horsemen, and conquering a vast number of vessels and cannon, etc. He also took on the following July 21 the royal castle and the city of Tunis with God's help, quite without losses, and plundered it. He drove out the Turkish [emperor's] Solyman's foremost captain and lieutenant at sea, called Barbarossa, with all his helpers from the kingdom of Tunis.../ Printed at Nuremberg, the imperial city / M./ C.S.D./ 31 August 1535.''

 The second is "Plan de la ville de Tunis et de ses environs, c. 1740-1749" map by Jacques-Nicolas Bellin (1703-1772). The third is description of the inner fortification of "la citadella di Tunisi" from an Italian source (dated around 1600-1699). Both are from the "Collection d'Anville", Bibliotheque nationale de France.


Ministere de l'enseignement superieur Presidence